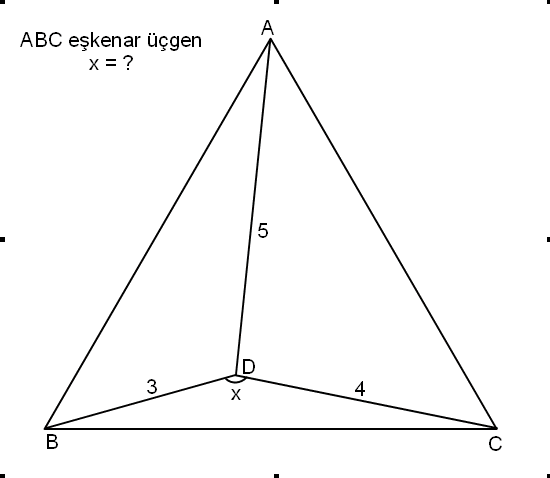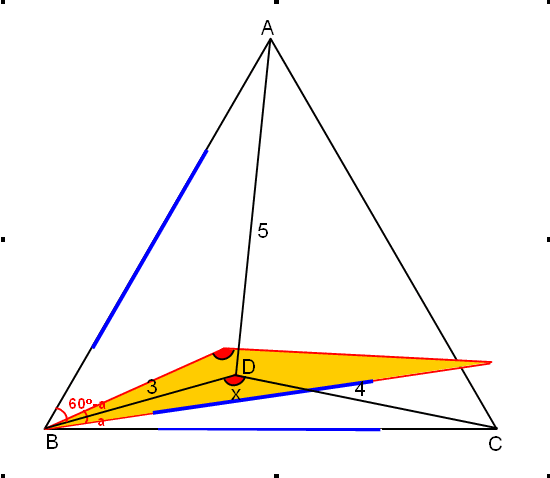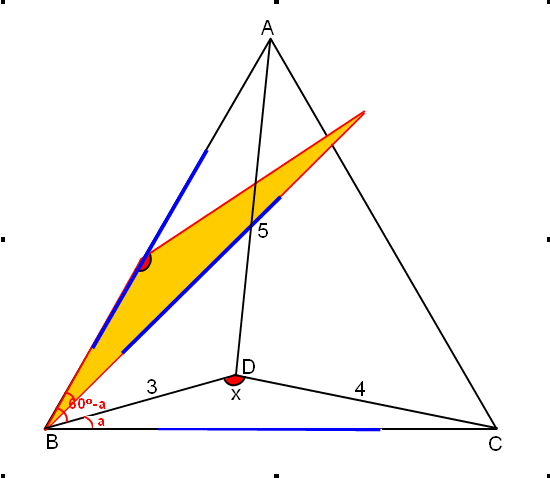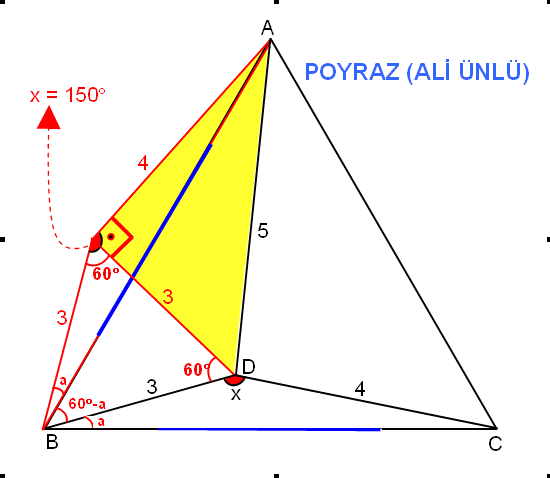
Eşkenar Üçgen

Eşkenar üçgen: Türkçede eşkenar üçgen anlamına gelen, yüzyıllardır matematikçileri ve sanatçıları büyüleyen bir geometrik harikadır. Bu makalede eşkenar üçgenlerin benzersiz özelliklerini inceleyeceğiz, matematiksel özelliklerini inceleyeceğiz ve çeşitli alanlarda oynadıkları rolü ortaya çıkaracağız. İster bir matematik tutkunu olun ister sadece geometrinin harikalarına meraklı olun, eşkenar üçgenin dünyasına yapılan bu yolculuk kesinlikle ilginizi çekecektir.

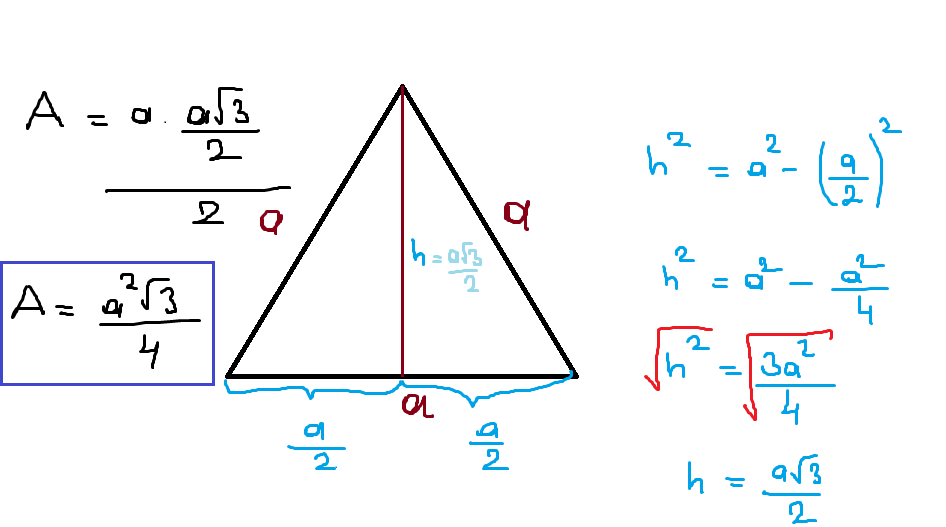
Geometri Açıklandı Eşkenar Üçgenlerin Özellikleri

Eşkenar üçgen, üç eşit kenar uzunluğu ve her biri 60 derecelik üç eşit iç açıyla karakterize edilen özel bir üçgen türüdür. Bu üçgenler, daha geniş üçgen kategorisinin bir alt kümesidir, ancak simetrileri ve dengeleri onları öne çıkarır. Eşkenar üçgeni hayalinizde canlandırmak için, üç kenarın ve açıların aynı olduğu bir ok ucu hayal edin. Bu doğal simetri, estetik çekiciliğe ve matematiksel zarafete katkıda bulunur.

Eşkenar üçgenin tanımlayıcı özelliklerini inceleyelim

1. Eşit Kenar Uzunlukları:
   • Eşkenar üçgende üç kenar da eşit uzunluktadır. Bu tekdüzelik üçgene uyumlu ve dengeli bir görünüm kazandırır.
2. Tutarlı İç Açılar:
   • Eşkenar üçgenin her bir iç açısının ölçüsü 60 derecedir. Herhangi bir üçgendeki üç açının toplamı her zaman 180 dereceye eşittir, yani eşkenar üçgende her açı toplamın üçte birine katkıda bulunur.
3. Simetri ve Estetik:
   • Eşkenar üçgenlerin simetrisi onları görsel olarak çekici kılmakta ve sanatta, mimaride ve tasarımda sıklıkla kullanılmasına yol açmaktadır. Antik uygarlıklardan modern yapılara kadar bu üçgenler çeşitli kültürlerin estetiğine damgasını vurmuştur.

Matematik Oyunda Eşkenar Üçgen’in Matematiksel Özelliklerini Keşfetmek

Eşkenar üçgenler matematiksel keşifler için zengin bir oyun alanı sunar. Bu üçgenlerle ilgili ilgi çekici matematiksel özelliklerden bazılarını inceleyelim:

1. Çevre ve Alan:
   • Eşkenar üçgenin çevresi, tüm kenarların eşit olması koşuluyla bir kenar uzunluğunun üç katıdır. Alan, A = (s^2 * √3) / 4 formülü kullanılarak hesaplanabilir; burada ‘s’, bir kenarın uzunluğunu temsil eder. Bu basit formüller eşkenar üçgenleri geometrik hesaplamaları öğrenmek ve anlamak için mükemmel bir başlangıç noktası haline getirir.
2. Merkez ve Medyanlar:
   • Eşkenar üçgenin ağırlık merkezi kenarortaylarının kesiştiği noktadır. Medyanlar, her köşeden karşı tarafın orta noktasına çizilen çizgilerdir. Eşkenar üçgende ağırlık merkezi her medyanı 2:1 oranında böler; yani ağırlık merkezinden tepe noktasına olan mesafe, ağırlık merkezinden orta noktaya olan mesafenin iki katıdır.
3. Yazılı Daire:
   • Eşkenar üçgenler, iç daire olarak da bilinen yazılı bir daireye mükemmel şekilde uyum sağlar. Bu dairenin yarıçapı üçgenin yüksekliğinin üçte birine eşittir. Bu özellik sadece görsel açıdan hoş olmakla kalmıyor, aynı zamanda çeşitli matematiksel uygulamalarda da önem taşıyor.

Geometrinin Ötesindeki Uygulamalar Gerçek Dünya Bağlamında Eşkenar Üçgenler

Eşkenar üçgenin etkisi geometri alanının çok ötesine uzanır. Eşkenar üçgenlerin çok önemli bir rol oynadığı bazı gerçek dünya uygulamaları:

1. Yapısal Kararlılık:
   • Mühendisler genellikle kafes kirişlerin ve çerçevelerin tasarımında eşkenar üçgenleri kullanırlar. Bu üçgenlerin doğal stabilitesi ve dengesi, onları yükleri eşit şekilde dağıtmak ve binaların ve köprülerin yapısal bütünlüğüne katkıda bulunmak için ideal kılar.
2. Sanat ve Tasarım:
   • Eşkenar üçgenler tarih boyunca sanat ve tasarımda tekrarlanan bir motif olmuştur. İslam sanatındaki mozaiklerden modern grafik tasarıma kadar eşkenar üçgenin simetrisi ve sadeliği onu görsel estetiğin çok yönlü bir unsuru haline getiriyor.
3. Şifreleme Algoritmaları:
   • Bilgisayar bilimi alanında eşkenar üçgenler belirli kriptografik algoritmalarda uygulama alanı bulur. Güvenli ve etkili şifreleme yöntemleri oluşturmak için benzersiz özelliklerinden yararlanılır.

Section	Key Points
Giriş	Eşkenar üçgenin Türkçe anlamı ve matematikçileri, sanatçıları büyüleyen geometrik bir harika olduğu vurgulanıyor.
Geometri Açıklandı	Eşkenar üçgenin özellikleri inceleniyor: eşit kenar uzunlukları, tutarlı iç açılar, simetri ve estetik.
Matematik Oyunda	Eşkenar üçgenin çevre, alan, merkez, medyanlar ve yazılı daire gibi matematiksel özellikleri keşfediliyor.
Geometrinin Ötesindeki Uygulamalar	Eşkenar üçgenin yapısal kararlılık, sanat ve tasarım, şifreleme algoritmaları gibi gerçek dünya uygulamaları ele alınıyor.
Sonuç	Eşkenar üçgenlerin matematik ve gerçek dünya arasındaki etkileşiminin zarif bir kanıtı olduğu vurgulanıyor.

Eşkenar Üçgenlerin Güzelliğini Kucaklamak

Sonuç olarak eşkenar üçgtr veya eşkenar üçgenler, matematik ile gerçek dünya arasındaki zarif etkileşimin bir kanıtıdır. Eşkenar üçgenler, geometrik mükemmelliklerinden çeşitli alanlardaki pratik uygulamalarına kadar zihinleri büyülemeye ve yaratıcılığa ilham vermeye devam ediyor. Bu üçgenlerin inceliklerini çözdükçe, yalnızca geometriye dair daha derin bir anlayış kazanmakla kalmıyoruz, aynı zamanda matematiksel kavramların doğasında var olan ebedi güzelliğin takdirini de kazanıyoruz.

Eşkenar Üçgen’in Trend Olduğu En İyi Bölgeler

Trabzon	100
Diyarbakır	86
Osmaniye	83
Gaziantep	79
Eskişehir Province	78
Kayseri Province	71
Giresun	69
Erzurum	68
Ankara	67
Hatay	66
Sivas	59
Van	58
Mersin Province	56
Denizli	50
Adana	44
Ordu	42
Konya	42
Tekirdağ	42
Antalya	37
Muğla	36
Samsun	35

Eşkenar Üçgen ile ilgili en çok sorulan sorular

İlgili Sorgular	Trend Yükselişi
geniş açılı üçgen	5000
21 dm kaç m	4999
52 m kaç dm	4998
2 basamaklı en büyük asal sayı	4997
52 m kaç dm dir	4996
ods eba	4995
900 mm kaç cm	4994
6,8 m kaç cm	4993
aritmetik ortalama	4992
21 dm kaç m dir	4991
52m kaç dm	4990
900mm kaç cm	4989
21dm kaç m	4988
52 metre kaç dm dir	4987
dikdörtgenin alanı	4986
2 basamaklı en küçük asal sayı	4985
0,04 km kac m	4984
0.04 km kaç metre	4983
dik ucgen	4982
52m kac dm	4981
900 mm kac cm	4980
mutlak degeri 1 ile 5 arasinda olan kac tane tam sayi vardir	4979
21 dm kac m	4978
birleşim işareti	4977
80 in yüzde 45 i kaçtır	4976